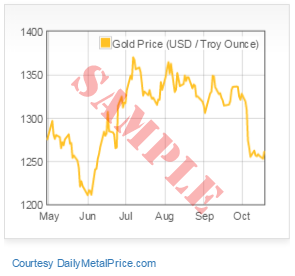
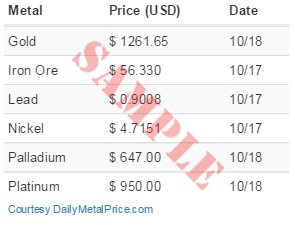
Archive: Daily Metal Prices in Bulgarian Lev
Access all previously published metal price data for multiple currencies going back to 2010. For USD rates our archive goes back to 2000 and can be accessed here.
Metal Prices in BGN
Dates with metal prices and corresponding currency exchange rates are shown. Click on any date to view the metal prices for that day using the currency rate and metal prices specific to that date. For the most comprehensive list of metals prices by date see our Metal Prices byDate Archive.
You can view the most current metal prices in BGN (Bulgarian Lev) here or click on an archived date below.
2010
Jul 16th Jul 19th Jul 20th Jul 21st Jul 22nd Jul 23rd Jul 26th Jul 27th Jul 28th Jul 29th Jul 30th Aug 2nd Aug 3rd Aug 4th Aug 5th Aug 6th Aug 9th Aug 10th Aug 11th Aug 12th Aug 13th Aug 16th Aug 17th Aug 18th Aug 19th Aug 20th Aug 23rd Aug 24th Aug 25th Aug 26th Aug 27th Aug 30th Aug 31st Sep 1st Sep 2nd Sep 3rd Sep 6th Sep 7th Sep 8th Sep 9th Sep 10th Sep 13th Sep 14th Sep 15th Sep 16th Sep 17th Sep 20th Sep 21st Sep 22nd Sep 23rd Sep 24th Sep 27th Sep 28th Sep 29th Sep 30th Oct 1st Oct 4th Oct 5th Oct 6th Oct 7th Oct 8th Oct 11th Oct 12th Oct 13th Oct 14th Oct 15th Oct 18th Oct 19th Oct 20th Oct 21st Oct 22nd Oct 25th Oct 26th Oct 27th Oct 28th Oct 29th Nov 1st Nov 2nd Nov 3rd Nov 4th Nov 5th Nov 8th Nov 9th Nov 10th Nov 11th Nov 12th Nov 15th Nov 16th Nov 17th Nov 18th Nov 19th Nov 22nd Nov 23rd Nov 24th Nov 25th Nov 26th Nov 29th Nov 30th Dec 1st Dec 2nd Dec 3rd Dec 6th Dec 7th Dec 8th Dec 10th Dec 13th Dec 14th Dec 15th Dec 16th Dec 17th Dec 20th Dec 21st Dec 22nd Dec 23rd Dec 24th Dec 27th Dec 28th Dec 29th Dec 30th Dec 31st
2011
Jan 3rd Jan 4th Jan 5th Jan 6th Jan 7th Jan 10th Jan 11th Jan 12th Jan 13th Jan 14th Jan 17th Jan 18th Jan 19th Jan 20th Jan 21st Jan 24th Jan 25th Jan 26th Jan 27th Jan 28th Jan 31st Feb 1st Feb 2nd Feb 3rd Feb 4th Feb 8th Feb 9th Feb 10th Feb 11th Feb 14th Feb 15th Feb 16th Feb 17th Feb 18th Feb 21st Feb 22nd Feb 23rd Feb 24th Feb 25th Feb 28th Mar 1st Mar 2nd Mar 3rd Mar 4th Mar 7th Mar 8th Mar 9th Mar 10th Mar 11th Mar 14th Mar 15th Mar 16th Mar 17th Mar 18th Mar 21st Mar 22nd Mar 23rd Mar 24th Mar 25th Mar 28th Mar 29th Mar 30th Mar 31st Apr 1st Apr 4th Apr 5th Apr 6th Apr 7th Apr 8th Apr 11th Apr 12th Apr 13th Apr 14th Apr 15th Apr 18th Apr 19th Apr 20th Apr 21st Apr 26th Apr 27th Apr 28th Apr 29th May 2nd May 3rd May 4th May 5th May 6th May 9th May 10th May 11th May 12th May 13th May 16th May 17th May 18th May 19th May 23rd May 24th May 25th May 26th May 27th May 30th May 31st Jun 1st Jun 2nd Jun 3rd Jun 6th Jun 7th Jun 8th Jun 9th Jun 10th Jun 13th Jun 14th Jun 15th Jun 16th Jun 17th Jun 20th Jun 21st Jun 22nd Jun 23rd Jun 24th Jun 27th Jun 28th Jun 29th Jun 30th Jul 1st Jul 4th Jul 5th Jul 6th Jul 7th Jul 8th Jul 11th Jul 12th Jul 13th Jul 14th Jul 15th Jul 18th Jul 19th Jul 20th Jul 21st Jul 22nd Jul 25th Jul 26th Jul 27th Jul 28th Jul 29th Aug 1st Aug 2nd Aug 3rd Aug 4th Aug 5th Aug 8th Aug 9th Aug 10th Aug 11th Aug 12th Aug 15th Aug 16th Aug 17th Aug 18th Aug 19th Aug 22nd Aug 23rd Aug 24th Aug 25th Aug 26th Aug 29th Aug 30th Aug 31st Sep 1st Sep 2nd Sep 5th Sep 6th Sep 7th Sep 8th Sep 9th Sep 12th Sep 13th Sep 14th Sep 15th Sep 16th Sep 19th Sep 20th Sep 21st Sep 22nd Sep 23rd Sep 26th Sep 27th Sep 28th Sep 29th Sep 30th Oct 3rd Oct 4th Oct 5th Oct 6th Oct 7th Oct 10th Oct 11th Oct 12th Oct 13th Oct 14th Oct 17th Oct 18th Oct 19th Oct 20th Oct 21st Oct 24th Oct 25th Oct 26th Oct 27th Oct 28th Oct 31st Nov 1st Nov 2nd Nov 3rd Nov 4th Nov 7th Nov 8th Nov 9th Nov 10th Nov 11th Nov 14th Nov 15th Nov 16th Nov 17th Nov 18th Nov 21st Nov 22nd Nov 23rd Nov 24th Nov 25th Nov 28th Nov 29th Nov 30th Dec 1st Dec 2nd Dec 5th Dec 6th Dec 7th Dec 8th Dec 9th Dec 12th Dec 13th Dec 14th Dec 15th Dec 16th Dec 19th Dec 20th Dec 21st Dec 22nd Dec 23rd Dec 27th Dec 28th Dec 29th Dec 30th
2012
Jan 2nd Jan 3rd Jan 4th Jan 5th Jan 6th Jan 9th Jan 10th Jan 11th Jan 12th Jan 13th Jan 16th Jan 17th Jan 18th Jan 19th Jan 20th Jan 23rd Jan 24th Jan 25th Jan 26th Jan 27th Jan 30th Jan 31st Feb 1st Feb 2nd Feb 3rd Feb 6th Feb 7th Feb 8th Feb 9th Feb 10th Feb 13th Feb 14th Feb 15th Feb 16th Feb 17th Feb 20th Feb 21st Feb 22nd Feb 23rd Feb 24th Feb 27th Feb 28th Feb 29th Mar 1st Mar 2nd Mar 5th Mar 6th Mar 7th Mar 8th Mar 9th Mar 12th Mar 13th Mar 14th Mar 15th Mar 16th Mar 19th Mar 20th Mar 21st Mar 22nd Mar 23rd Mar 26th Mar 27th Mar 28th Mar 29th Mar 30th Apr 2nd Apr 4th Apr 5th Apr 10th Apr 11th Apr 12th Apr 13th Apr 16th Apr 17th Apr 18th Apr 19th Apr 20th Apr 23rd Apr 24th Apr 25th Apr 26th Apr 27th Apr 30th May 2nd May 3rd May 4th May 7th May 8th May 9th May 10th May 11th May 14th May 15th May 16th May 17th May 18th May 21st May 22nd May 23rd May 24th May 25th May 28th May 29th May 30th May 31st Jun 1st Jun 4th Jun 5th Jun 6th Jun 7th Jun 8th Jun 11th Jun 12th Jun 13th Jun 14th Jun 15th Jun 18th Jun 19th Jun 20th Jun 21st Jun 22nd Jun 25th Jun 26th Jun 27th Jun 28th Jun 29th Jul 2nd Jul 3rd Jul 4th Jul 5th Jul 6th Jul 9th Jul 10th Jul 11th Jul 12th Jul 13th Jul 16th Jul 17th Jul 18th Jul 19th Jul 20th Jul 23rd Jul 24th Jul 25th Jul 26th Jul 27th Jul 30th Jul 31st Aug 1st Aug 2nd Aug 3rd Aug 6th Aug 7th Aug 8th Aug 9th Aug 10th Aug 13th Aug 14th Aug 15th Aug 16th Aug 17th Aug 20th Aug 21st Aug 22nd Aug 23rd Aug 24th Aug 27th Aug 28th Aug 29th Aug 30th Aug 31st Sep 3rd Sep 4th Sep 5th Sep 6th Sep 7th Sep 10th Sep 11th Sep 12th Sep 13th Sep 17th Sep 18th Sep 19th Sep 21st Sep 24th Sep 25th Sep 27th Sep 28th Oct 1st Oct 2nd Oct 3rd Oct 4th Oct 5th Oct 8th Oct 9th Oct 10th Oct 11th Oct 12th Oct 15th Oct 16th Oct 17th Oct 18th Oct 19th Oct 22nd Oct 23rd Oct 24th Oct 25th Oct 26th Oct 29th Oct 30th Oct 31st Nov 1st Nov 2nd Nov 5th Nov 6th Nov 7th Nov 8th Nov 9th Nov 12th Nov 13th Nov 14th Nov 15th Nov 16th Nov 19th Nov 20th Nov 21st Nov 22nd Nov 23rd Nov 26th Nov 27th Nov 28th Nov 29th Nov 30th Dec 3rd Dec 4th Dec 5th Dec 6th Dec 7th Dec 10th Dec 11th Dec 12th Dec 13th Dec 14th Dec 17th Dec 18th Dec 19th Dec 20th Dec 21st Dec 24th Dec 27th Dec 28th Dec 31st
2013
Jan 2nd Jan 3rd Jan 4th Jan 7th Jan 8th Jan 9th Jan 10th Jan 11th Jan 14th Jan 15th Jan 16th Jan 17th Jan 18th Jan 21st Jan 22nd Jan 23rd Jan 24th Jan 25th Jan 28th Jan 29th Jan 30th Jan 31st Feb 1st Feb 4th Feb 5th Feb 6th Feb 7th Feb 8th Feb 11th Feb 12th Feb 13th Feb 14th Feb 15th Feb 18th Feb 19th Feb 20th Feb 21st Feb 22nd Feb 25th Feb 26th Feb 27th Feb 28th Mar 1st Mar 4th Mar 5th Mar 6th Mar 7th Mar 8th Mar 11th Mar 12th Mar 13th Mar 14th Mar 15th Mar 18th Mar 19th Mar 20th Mar 21st Mar 22nd Mar 25th Mar 26th Mar 27th Mar 28th Apr 2nd Apr 3rd Apr 4th Apr 5th Apr 8th Apr 9th Apr 10th Apr 11th Apr 12th Apr 15th Apr 16th Apr 17th Apr 18th Apr 19th Apr 22nd Apr 23rd Apr 24th Apr 25th Apr 29th Apr 30th May 2nd May 3rd May 6th May 7th May 8th May 9th May 10th May 13th May 14th May 15th May 16th May 17th May 20th May 21st May 22nd May 23rd May 24th May 27th May 28th May 29th May 30th May 31st Jun 3rd Jun 4th Jun 5th Jun 6th Jun 7th Jun 10th Jun 11th Jun 12th Jun 13th Jun 14th Jun 17th Jun 18th Jun 19th Jun 20th Jun 21st Jun 24th Jun 25th Jun 26th Jun 27th Jun 28th Jul 1st Jul 2nd Jul 3rd Jul 4th Jul 5th Jul 8th Jul 9th Jul 10th Jul 11th Jul 12th Jul 15th Jul 16th Jul 18th Jul 19th Jul 22nd Jul 23rd Jul 24th Jul 25th Jul 26th Jul 29th Jul 30th Jul 31st Aug 1st Aug 2nd Aug 5th Aug 6th Aug 7th Aug 8th Aug 9th Aug 12th Aug 13th Aug 14th Aug 15th Aug 16th Aug 19th Aug 20th Aug 21st Aug 22nd Aug 23rd Aug 26th Aug 27th Aug 28th Aug 29th Aug 30th Sep 2nd Sep 3rd Sep 4th Sep 5th Sep 6th Sep 9th Sep 10th Sep 11th Sep 12th Sep 13th Sep 16th Sep 17th Sep 18th Sep 19th Sep 20th Sep 23rd Sep 24th Sep 25th Sep 26th Sep 27th Sep 30th Oct 1st Oct 2nd Oct 3rd Oct 4th Oct 7th Oct 8th Oct 9th Oct 10th Oct 11th Oct 14th Oct 15th Oct 16th Oct 17th Oct 18th Oct 21st Oct 22nd Oct 23rd Oct 24th Oct 25th Oct 28th Oct 29th Oct 30th Oct 31st Nov 1st Nov 4th Nov 5th Nov 6th Nov 7th Nov 8th Nov 11th Nov 12th Nov 13th Nov 14th Nov 15th Nov 18th Nov 19th Nov 20th Nov 21st Nov 22nd Nov 25th Nov 26th Nov 27th Nov 28th Nov 29th Dec 2nd Dec 3rd Dec 4th Dec 5th Dec 6th Dec 9th Dec 10th Dec 11th Dec 12th Dec 13th Dec 16th Dec 17th Dec 18th Dec 19th Dec 20th Dec 23rd Dec 24th Dec 27th Dec 30th Dec 31st
2014
Jan 2nd Jan 3rd Jan 6th Jan 7th Jan 8th Jan 9th Jan 10th Jan 13th Jan 14th Jan 15th Jan 16th Jan 17th Jan 20th Jan 21st Jan 22nd Jan 23rd Jan 24th Jan 27th Jan 28th Jan 29th Jan 30th Jan 31st Feb 3rd Feb 4th Feb 5th Feb 6th Feb 7th Feb 10th Feb 11th Feb 12th Feb 13th Feb 14th Feb 17th Feb 18th Feb 19th Feb 20th Feb 21st Feb 24th Feb 25th Feb 26th Feb 27th Feb 28th Mar 3rd Mar 4th Mar 5th Mar 6th Mar 7th Mar 10th Mar 11th Mar 12th Mar 13th Mar 14th Mar 17th Mar 18th Mar 19th Mar 20th Mar 21st Mar 24th Mar 25th Mar 26th Mar 27th Mar 28th Mar 31st Apr 1st Apr 2nd Apr 3rd Apr 4th Apr 7th Apr 8th Apr 9th Apr 10th Apr 11th Apr 14th Apr 15th Apr 16th Apr 17th Apr 22nd Apr 23rd Apr 24th Apr 25th Apr 28th Apr 29th Apr 30th May 2nd May 5th May 6th May 7th May 8th May 9th May 12th May 13th May 14th May 15th May 16th May 19th May 20th May 21st Jun 4th Jun 5th Jun 6th Jun 9th Jun 10th Jun 11th Jun 12th Jun 13th Jun 16th Jun 17th Jun 18th Jun 19th Jun 20th Jun 23rd Jun 24th Jun 25th Jun 26th Jun 27th Jun 30th Jul 1st Jul 2nd Jul 3rd Jul 4th Jul 7th Jul 8th Jul 9th Jul 10th Jul 11th Jul 14th Jul 15th Jul 16th Jul 17th Jul 18th Jul 21st Jul 22nd Jul 23rd Jul 24th Jul 25th Jul 28th Jul 29th Jul 30th Jul 31st Aug 1st Aug 4th Aug 5th Aug 6th Aug 7th Aug 8th Aug 11th Aug 12th Aug 13th Aug 14th Aug 15th Aug 18th Aug 19th Aug 20th Aug 21st Aug 22nd Aug 25th Aug 26th Aug 27th Aug 28th Aug 29th Sep 1st Sep 2nd Sep 3rd Sep 4th Sep 5th Sep 8th Sep 9th Sep 10th Sep 11th Sep 12th Sep 15th Sep 16th Sep 17th Sep 18th Sep 19th Sep 22nd Sep 23rd Sep 24th Sep 25th Sep 26th Sep 30th Oct 1st Oct 2nd Oct 3rd Oct 6th Oct 7th Oct 8th Oct 9th Oct 10th Oct 13th Oct 14th Oct 15th Oct 16th Oct 17th Oct 20th Oct 21st Oct 22nd Oct 23rd Oct 24th Oct 27th Oct 28th Oct 29th Oct 30th Oct 31st Nov 3rd Nov 4th Nov 5th Nov 6th Nov 7th Nov 10th Nov 11th Nov 12th Nov 13th Nov 14th Nov 17th Nov 18th Nov 19th Nov 20th Nov 21st Nov 24th Nov 25th Nov 26th Nov 27th Nov 28th Dec 1st Dec 2nd Dec 3rd Dec 4th Dec 5th Dec 8th Dec 9th Dec 10th Dec 11th Dec 12th Dec 15th Dec 16th Dec 17th Dec 18th Dec 19th Dec 22nd Dec 23rd Dec 24th Dec 29th Dec 30th Dec 31st
2015
Jan 2nd Jan 5th Jan 6th Jan 7th Jan 8th Jan 9th Jan 12th Jan 13th Jan 14th Jan 15th Jan 16th Jan 19th Jan 20th Jan 21st Jan 22nd Jan 23rd Jan 26th Jan 27th Jan 28th Jan 29th Jan 30th Feb 2nd Feb 3rd Feb 4th Feb 5th Feb 6th Feb 9th Feb 10th Feb 11th Feb 12th Feb 13th Feb 16th Feb 17th Feb 18th Feb 19th Feb 20th Feb 23rd Feb 24th Feb 25th Feb 26th Feb 27th Mar 2nd Mar 3rd Mar 4th Mar 5th Mar 6th Mar 9th Mar 10th Mar 11th Mar 12th Mar 13th Mar 16th Mar 17th Mar 18th Mar 19th Mar 20th Mar 23rd Mar 24th Mar 25th Mar 26th Mar 27th Mar 30th Mar 31st Apr 1st Apr 2nd Apr 7th Apr 8th Apr 9th Apr 10th Apr 13th Apr 14th Apr 15th Apr 16th Apr 17th Apr 20th Apr 21st Apr 22nd Apr 23rd Apr 24th Apr 27th Apr 28th Apr 29th Apr 30th May 4th May 5th May 6th May 7th May 8th May 11th May 12th May 13th May 14th May 15th May 18th May 19th May 20th May 21st May 22nd May 25th May 26th May 27th May 28th May 29th Jun 1st Jun 2nd Jun 3rd Jun 4th Jun 5th Jun 8th Jun 9th Jun 10th Jun 11th Jun 12th Jun 15th Jun 16th Jun 17th Jun 18th Jun 19th Jun 22nd Jun 23rd Jun 24th Jun 25th Jun 26th Jun 29th Jun 30th Jul 1st Jul 2nd Jul 3rd Jul 6th Jul 7th Jul 8th Jul 9th Jul 10th Jul 13th Jul 14th Jul 15th Jul 16th Jul 17th Jul 20th Jul 21st Jul 22nd Jul 23rd Jul 24th Jul 27th Jul 28th Jul 29th Jul 30th Jul 31st Aug 3rd Aug 4th Aug 5th Aug 6th Aug 7th Aug 10th Aug 11th Aug 12th Aug 13th Aug 14th Aug 17th Aug 18th Aug 19th Aug 20th Aug 21st Aug 24th Aug 25th Aug 26th Aug 27th Aug 28th Aug 31st Sep 1st Sep 2nd Sep 3rd Sep 4th Sep 7th Sep 8th Sep 9th Sep 10th Sep 11th Sep 14th Sep 15th Sep 16th Sep 17th Sep 18th Sep 21st Sep 22nd Sep 23rd Sep 24th Sep 25th Sep 28th Sep 29th Sep 30th Oct 1st Oct 2nd Oct 5th Oct 6th Oct 7th Oct 8th Oct 9th Oct 12th Oct 13th Oct 14th Oct 15th Oct 16th Oct 19th Oct 20th Oct 21st Oct 22nd Oct 23rd Oct 26th Oct 27th Oct 28th Oct 29th Oct 30th Nov 2nd Nov 3rd Nov 4th Nov 5th Nov 6th Nov 9th Nov 10th Nov 11th Nov 12th Nov 13th Nov 16th Nov 17th Nov 18th Nov 19th Nov 20th Nov 23rd Nov 24th Nov 25th Nov 26th Nov 27th Nov 30th Dec 1st Dec 2nd Dec 3rd Dec 4th Dec 7th Dec 8th Dec 9th Dec 10th Dec 11th Dec 14th Dec 15th Dec 16th Dec 17th Dec 18th Dec 21st Dec 22nd Dec 23rd Dec 24th Dec 28th Dec 29th Dec 30th Dec 31st
2016
Jan 4th Jan 5th Jan 6th Jan 7th Jan 8th Jan 11th Jan 12th Jan 13th Jan 14th Jan 15th Jan 18th Jan 19th Jan 20th Jan 21st Jan 22nd Jan 25th Jan 26th Jan 27th Jan 28th Jan 29th Feb 1st Feb 2nd Feb 3rd Feb 4th Feb 5th Feb 8th Feb 9th Feb 10th Feb 11th Feb 12th Feb 15th Feb 16th Feb 17th Feb 18th Feb 19th Feb 22nd Feb 23rd Feb 24th Feb 25th Feb 26th Feb 29th Mar 1st Mar 2nd Mar 3rd Mar 4th Mar 7th Mar 8th Mar 9th Mar 10th Mar 11th Mar 14th Mar 15th Mar 16th Mar 17th Mar 18th Mar 21st Mar 22nd Mar 23rd Mar 24th Mar 29th Mar 30th Mar 31st Apr 1st Apr 4th Apr 5th Apr 6th Apr 7th Apr 8th Apr 11th Apr 12th Apr 13th Apr 14th Apr 15th Apr 18th Apr 19th Apr 20th Apr 21st Apr 22nd Apr 25th Apr 26th Apr 27th Apr 28th Apr 29th May 2nd May 3rd May 4th May 5th May 6th May 9th May 10th May 11th May 12th May 13th May 16th May 17th May 18th May 19th May 20th May 23rd May 24th May 25th May 26th May 27th May 30th May 31st Jun 1st Jun 2nd Jun 3rd Jun 6th Jun 7th Jun 8th Jun 9th Jun 10th Jun 13th Jun 14th Jun 15th Jun 16th Jun 17th Jun 20th Jun 21st Jun 22nd Jun 23rd Jun 24th Jun 27th Jun 28th Jun 29th Jun 30th Jul 1st Jul 4th Jul 5th Jul 6th Jul 7th Jul 8th Jul 11th Jul 12th Jul 13th Jul 14th Jul 15th Jul 18th Jul 19th Jul 20th Jul 21st Jul 22nd Jul 25th Jul 26th Jul 27th Jul 28th Jul 29th Aug 1st Aug 2nd Aug 3rd Aug 4th Aug 5th Aug 8th Aug 9th Aug 10th Aug 11th Aug 12th Aug 15th Aug 16th Aug 17th Aug 18th Aug 19th Aug 22nd Aug 23rd Aug 24th Aug 25th Aug 26th Aug 29th Aug 30th Aug 31st Sep 1st Sep 2nd Sep 5th Sep 6th Sep 7th Sep 8th Sep 9th Sep 12th Sep 13th Sep 14th Sep 15th Sep 16th Sep 19th Sep 20th Sep 21st Sep 22nd Sep 23rd Sep 26th Sep 27th Sep 28th Sep 29th Sep 30th Oct 3rd Oct 4th Oct 5th Oct 6th Oct 7th Oct 10th Oct 11th Oct 12th Oct 13th Oct 14th Oct 17th Oct 18th Oct 19th Oct 20th Oct 21st Oct 24th Oct 25th Oct 26th Oct 27th Oct 28th Oct 31st Nov 1st Nov 2nd Nov 3rd Nov 4th Nov 7th Nov 8th Nov 9th Nov 10th Nov 11th Nov 14th Nov 15th Nov 16th Nov 17th Nov 18th Nov 21st Nov 22nd Nov 23rd Nov 24th Nov 25th Nov 28th Nov 29th Nov 30th Dec 1st Dec 2nd Dec 5th Dec 6th Dec 7th Dec 8th Dec 9th Dec 12th Dec 13th Dec 14th Dec 15th Dec 16th Dec 19th Dec 20th Dec 21st Dec 22nd Dec 23rd Dec 27th Dec 28th Dec 29th Dec 30th
2017
Jan 2nd Jan 3rd Jan 4th Jan 5th Jan 6th Jan 9th Jan 10th Jan 11th Jan 12th Jan 13th Jan 16th Jan 17th Jan 18th Jan 19th Jan 20th Jan 23rd Jan 24th Jan 25th Jan 26th Jan 27th Jan 30th Jan 31st Feb 1st Feb 2nd Feb 3rd Feb 6th Feb 7th Feb 8th Feb 9th Feb 10th Feb 13th Feb 14th Feb 15th Feb 16th Feb 17th Feb 20th Feb 21st Feb 22nd Feb 23rd Feb 24th Feb 27th Feb 28th Mar 1st Mar 2nd Mar 3rd Mar 6th Mar 7th Mar 8th Mar 9th Mar 10th Mar 13th Mar 14th Mar 15th Mar 16th Mar 17th Mar 20th Mar 21st Mar 22nd Mar 23rd Mar 24th Mar 27th Mar 28th Mar 29th Mar 30th Mar 31st Apr 3rd Apr 4th Apr 5th Apr 6th Apr 7th Apr 10th Apr 11th Apr 12th Apr 13th Apr 18th Apr 19th Apr 20th Apr 21st Apr 24th Apr 25th Apr 26th Apr 27th Apr 28th May 2nd May 3rd May 4th May 5th May 8th May 9th May 10th May 11th May 12th May 15th May 16th May 17th May 18th May 19th May 22nd May 23rd May 24th May 25th May 26th May 29th May 30th May 31st Jun 1st Jun 2nd Jun 5th Jun 6th Jun 7th Jun 8th Jun 9th Jun 12th Jun 13th Jun 14th Jun 15th Jun 16th Jun 19th Jun 20th Jun 21st Jun 22nd Jun 23rd Jun 26th Jun 27th Jun 29th Jun 30th Jul 3rd Jul 4th Jul 5th Jul 6th Jul 7th Jul 10th Jul 11th Jul 12th Jul 13th Jul 14th Jul 17th Jul 18th Jul 19th Jul 20th Jul 21st Jul 24th Jul 25th Jul 26th Jul 27th Jul 28th Jul 31st Aug 1st Aug 2nd Aug 3rd Aug 4th Aug 7th Aug 8th Aug 9th Aug 10th Aug 11th Aug 14th Aug 15th Aug 16th Aug 17th Aug 18th Aug 21st Aug 22nd Aug 23rd Aug 24th Aug 25th Aug 28th Aug 29th Aug 30th Aug 31st Sep 1st Sep 4th Sep 5th Sep 6th Sep 7th Sep 8th Sep 11th Sep 12th Sep 13th Sep 14th Sep 15th Sep 18th Sep 19th Sep 20th Sep 21st Sep 22nd Sep 25th Sep 26th Sep 27th Sep 28th Sep 29th Oct 2nd Oct 3rd Oct 4th Oct 5th Oct 6th Oct 9th Oct 10th Oct 11th Oct 12th Oct 13th Oct 16th Oct 17th Oct 18th Oct 19th Oct 20th Oct 23rd Oct 24th Oct 25th Oct 26th Oct 27th Oct 30th Oct 31st Nov 1st Nov 2nd Nov 3rd Nov 6th Nov 7th Nov 8th Nov 9th Nov 10th Nov 13th Nov 14th Nov 15th Nov 16th Nov 17th Nov 20th Nov 21st Nov 22nd Nov 23rd Nov 24th Nov 27th Nov 28th Nov 29th Dec 1st Dec 4th Dec 5th Dec 6th Dec 7th Dec 8th Dec 11th Dec 12th Dec 13th Dec 14th Dec 15th Dec 18th Dec 19th Dec 20th Dec 21st Dec 22nd Dec 27th Dec 28th Dec 29th
2018
Jan 2nd Jan 3rd Jan 4th Jan 5th Jan 8th Jan 9th Jan 10th Jan 11th Jan 12th Jan 15th Jan 16th Jan 17th Jan 18th Jan 19th Jan 22nd Jan 23rd Jan 24th Jan 25th Jan 26th Jan 29th Jan 30th Jan 31st Feb 1st Feb 2nd Feb 5th Feb 6th Feb 7th Feb 8th Feb 9th Feb 12th Feb 13th Feb 14th Feb 15th Feb 16th Feb 19th Feb 20th Feb 21st Feb 22nd Feb 23rd Feb 26th Feb 27th Feb 28th Mar 1st Mar 2nd Mar 5th Mar 6th Mar 7th Mar 8th Mar 9th Mar 12th Mar 13th Mar 14th Mar 15th Mar 16th Mar 19th Mar 20th Mar 21st Mar 22nd Mar 23rd Mar 26th Mar 27th Mar 28th Mar 29th Mar 30th Apr 2nd Apr 3rd Apr 4th Apr 5th Apr 6th Apr 9th Apr 10th Apr 11th Apr 12th Apr 13th Apr 16th Apr 17th Apr 18th Apr 19th Apr 20th Apr 23rd Apr 24th Apr 25th Apr 26th Apr 27th Apr 30th May 1st May 2nd May 3rd May 4th May 7th May 8th May 9th May 10th May 11th May 14th May 15th May 16th May 17th May 18th May 21st May 22nd May 23rd May 24th May 25th May 28th May 29th May 30th May 31st Jun 1st Jun 4th Jun 5th Jun 6th Jun 7th Jun 8th Jun 11th Jun 12th Jun 13th Jun 14th Jun 15th Jun 18th Jun 19th Jun 20th Jun 21st Jun 22nd Jun 25th Jun 26th Jun 27th Jun 28th Jun 29th Jul 2nd Jul 3rd Jul 4th Jul 5th Jul 6th Jul 9th Jul 10th Jul 11th Jul 12th Jul 13th Jul 16th Jul 17th Jul 18th Jul 19th Jul 20th Jul 23rd Jul 24th Jul 25th Jul 26th Jul 27th Jul 30th Jul 31st Aug 1st Aug 2nd Aug 3rd Aug 6th Aug 7th Aug 8th Aug 9th Aug 10th Aug 13th Aug 14th Aug 15th Aug 16th Aug 17th Aug 20th Aug 21st Aug 22nd Aug 23rd Aug 24th Aug 27th Aug 28th Aug 29th Aug 30th Aug 31st Sep 3rd Sep 4th Sep 5th Sep 6th Sep 7th Sep 10th Sep 11th Sep 12th Sep 13th Sep 14th Sep 17th Sep 18th Sep 19th Sep 20th Sep 21st Sep 24th Sep 25th Sep 26th Sep 27th Sep 28th Oct 1st Oct 2nd Oct 3rd Oct 4th Oct 5th Oct 8th Oct 9th Oct 10th Oct 11th Oct 12th Oct 15th Oct 16th Oct 17th Oct 18th Oct 19th Oct 22nd Oct 23rd Oct 24th Oct 25th Oct 26th Oct 29th Oct 30th Oct 31st Nov 1st Nov 2nd Nov 5th Nov 6th Nov 7th Nov 8th Nov 9th Nov 12th Nov 13th Nov 14th Nov 15th Nov 16th Nov 19th Nov 20th Nov 21st Nov 22nd Nov 23rd Nov 26th Nov 27th Nov 28th Nov 29th Nov 30th Dec 3rd Dec 4th Dec 5th Dec 6th Dec 7th Dec 10th Dec 11th Dec 12th Dec 13th Dec 14th Dec 17th Dec 18th Dec 19th Dec 20th Dec 21st Dec 22nd Dec 24th Dec 26th Dec 27th Dec 28th Dec 31st
2019
Jan 2nd Jan 3rd Jan 4th Jan 7th Jan 8th Jan 9th Jan 10th Jan 11th Jan 14th Jan 15th Jan 16th Jan 17th Jan 18th Jan 21st Jan 22nd Jan 23rd Jan 24th Jan 25th Jan 28th Jan 29th Jan 30th Jan 31st Feb 1st Feb 4th Feb 5th Feb 6th Feb 7th Feb 8th Feb 11th Feb 12th Feb 13th Feb 14th Feb 15th Feb 18th Feb 19th Feb 20th Feb 21st Feb 22nd Feb 25th Feb 26th Feb 27th Feb 28th Mar 1st Mar 4th Mar 5th Mar 6th Mar 7th Mar 8th Mar 11th Mar 12th Mar 13th Mar 14th Mar 15th Mar 18th Mar 19th Mar 20th Mar 21st Mar 22nd Mar 25th Mar 26th Mar 27th Mar 28th Mar 29th Apr 1st Apr 2nd Apr 3rd Apr 4th Apr 5th Apr 8th Apr 9th Apr 10th Apr 11th Apr 12th Apr 15th Apr 16th Apr 17th Apr 18th Apr 19th Apr 22nd Apr 23rd Apr 24th Apr 25th Apr 26th Apr 29th Apr 30th May 2nd May 3rd May 6th May 7th May 8th May 9th May 10th May 11th May 13th May 14th May 15th May 16th May 17th May 20th May 21st May 22nd May 23rd May 24th May 27th May 28th May 29th May 30th May 31st Jun 3rd Jun 4th Jun 5th Jun 6th Jun 7th Jun 10th Jun 11th Jun 12th Jun 13th Jun 14th Jun 17th Jun 18th Jun 19th Jun 20th Jun 21st Jun 24th Jun 25th Jun 26th Jun 27th Jun 28th Jul 1st Jul 2nd Jul 3rd Jul 4th Jul 5th Jul 8th Jul 9th Jul 10th Jul 11th Jul 12th Jul 15th Jul 16th Jul 17th Jul 18th Jul 19th Jul 22nd Jul 23rd Jul 24th Jul 25th Jul 26th Jul 29th Jul 30th Jul 31st Aug 1st Aug 2nd Aug 5th Aug 6th Aug 7th Aug 8th Aug 9th Aug 12th Aug 13th Aug 14th Aug 15th Aug 16th Aug 19th Aug 20th Aug 21st Aug 22nd Aug 23rd Aug 26th Aug 27th Aug 28th Aug 29th Aug 30th Sep 2nd Sep 3rd Sep 4th Sep 5th Sep 6th Sep 9th Sep 10th Sep 11th Sep 12th Sep 13th Sep 16th Sep 17th Sep 18th Sep 19th Sep 20th Sep 23rd Sep 24th Sep 25th Sep 26th Sep 27th Sep 30th Oct 1st Oct 2nd Oct 3rd Oct 4th Oct 7th Oct 8th Oct 9th Oct 10th Oct 11th Oct 14th Oct 15th Oct 16th Oct 17th Oct 18th Oct 21st Oct 22nd Oct 23rd Oct 24th Oct 25th Oct 28th Oct 29th Oct 30th Oct 31st Nov 1st Nov 4th Nov 5th Nov 6th Nov 7th Nov 8th Nov 11th Nov 12th Nov 13th Nov 14th Nov 15th Nov 18th Nov 19th Nov 20th Nov 21st Nov 22nd Nov 25th Nov 26th Nov 27th Nov 28th Nov 29th Dec 2nd Dec 3rd Dec 4th Dec 5th Dec 6th Dec 9th Dec 10th Dec 11th Dec 12th Dec 13th Dec 16th Dec 17th Dec 18th Dec 19th Dec 20th Dec 23rd Dec 24th Dec 27th Dec 30th Dec 31st
2020
Jan 2nd Jan 3rd Jan 6th Jan 7th Jan 8th Jan 9th Jan 10th Jan 13th Jan 14th Jan 15th Jan 16th Jan 17th Jan 20th Jan 21st Jan 22nd Jan 23rd Jan 24th Jan 27th Jan 28th Jan 29th Jan 30th Jan 31st Feb 3rd Feb 4th Feb 5th Feb 6th Feb 7th Feb 10th Feb 11th Feb 12th Feb 13th Feb 14th Feb 17th Feb 18th Feb 19th Feb 20th Feb 21st Feb 24th Feb 25th Feb 26th Feb 27th Feb 28th Mar 2nd Mar 3rd Mar 4th Mar 5th Mar 6th Mar 9th Mar 10th Mar 11th Mar 12th Mar 13th Mar 16th Mar 17th Mar 18th Mar 19th Mar 20th Mar 23rd Mar 24th Mar 25th Mar 26th Mar 27th Mar 30th Mar 31st Apr 1st Apr 2nd Apr 3rd Apr 6th Apr 7th Apr 8th Apr 9th Apr 10th Apr 14th Apr 15th Apr 16th Apr 17th Apr 20th Apr 21st Apr 22nd Apr 23rd Apr 24th Apr 27th Apr 28th Apr 29th Apr 30th May 4th May 5th May 6th May 7th May 8th May 11th May 12th May 13th May 14th May 15th May 18th May 19th May 20th May 21st May 22nd May 25th May 26th May 27th May 28th May 29th Jun 1st Jun 2nd Jun 3rd Jun 4th Jun 5th Jun 8th Jun 9th Jun 10th Jun 11th Jun 12th Jun 15th Jun 16th Jun 17th Jun 18th Jun 19th Jun 22nd Jun 23rd Jun 24th Jun 25th Jun 26th Jun 29th Jun 30th Jul 1st Jul 2nd Jul 3rd Jul 6th Jul 7th Jul 8th Jul 9th Jul 10th Jul 13th Jul 14th Jul 15th Jul 16th Jul 17th Jul 20th Jul 21st Jul 22nd Jul 23rd Jul 24th Jul 27th Jul 28th Jul 29th Jul 30th Jul 31st Aug 3rd Aug 4th Aug 5th Aug 6th Aug 7th Aug 10th Aug 11th Aug 12th Aug 13th Aug 14th Aug 17th Aug 18th Aug 19th Aug 20th Aug 21st Aug 24th Aug 25th Aug 26th Aug 27th Aug 28th Aug 31st Sep 1st Sep 2nd Sep 3rd Sep 4th Sep 7th Sep 8th Sep 9th Sep 10th Sep 11th Sep 14th Sep 15th Sep 16th Sep 17th Sep 18th Sep 21st Sep 22nd Sep 23rd Sep 24th Sep 25th Sep 28th Sep 29th Sep 30th Oct 1st Oct 2nd Oct 5th Oct 6th Oct 7th Oct 8th Oct 9th Oct 12th Oct 13th Oct 14th Oct 15th Oct 16th Oct 19th Oct 20th Oct 21st Oct 22nd Oct 23rd Oct 26th Oct 27th Oct 28th Oct 29th Oct 30th Nov 2nd Nov 3rd Nov 4th Nov 5th Nov 6th Nov 9th Nov 10th Nov 11th Nov 12th Nov 13th Nov 16th Nov 17th Nov 18th Nov 19th Nov 20th Nov 23rd Nov 24th Nov 25th Nov 26th Nov 27th Nov 30th Dec 1st Dec 2nd Dec 3rd Dec 4th Dec 7th Dec 8th Dec 9th Dec 10th Dec 11th Dec 14th Dec 15th Dec 16th Dec 17th Dec 18th Dec 21st Dec 22nd Dec 23rd Dec 24th Dec 28th Dec 29th Dec 30th Dec 31st
2021
Jan 4th Jan 5th Jan 6th Jan 7th Jan 8th Jan 11th Jan 12th Jan 13th Jan 14th Jan 15th Jan 16th Jan 18th Jan 19th Jan 20th Jan 21st Jan 22nd Jan 25th Jan 26th Jan 27th Jan 28th Jan 29th Feb 1st Feb 2nd Feb 3rd Feb 4th Feb 5th Feb 8th Feb 9th Feb 10th Feb 11th Feb 12th Feb 15th Feb 16th Feb 17th Feb 18th Feb 19th Feb 22nd Feb 23rd Feb 24th Feb 25th Feb 26th Mar 1st Mar 2nd Mar 3rd Mar 4th Mar 5th Mar 8th Mar 9th Mar 10th Mar 11th Mar 12th Mar 15th Mar 16th Mar 17th Mar 18th Mar 19th Mar 22nd Mar 23rd Mar 24th Mar 25th Mar 26th Mar 29th Mar 30th Mar 31st Apr 1st Apr 2nd Apr 5th Apr 6th Apr 7th Apr 8th Apr 9th Apr 12th Apr 13th Apr 14th Apr 15th Apr 16th Apr 19th Apr 20th Apr 21st Apr 22nd Apr 23rd Apr 26th Apr 27th Apr 28th Apr 29th Apr 30th May 3rd May 4th May 5th May 6th May 7th May 10th May 11th May 12th May 13th May 14th May 17th May 18th May 19th May 20th May 21st May 24th May 25th May 26th May 27th May 28th May 31st Jun 1st Jun 2nd Jun 3rd Jun 4th Jun 7th Jun 8th Jun 9th Jun 10th Jun 11th Jun 14th Jun 15th Jun 16th Jun 17th Jun 18th Jun 21st Jun 22nd Jun 23rd Jun 24th Jun 25th Jun 28th Jun 29th Jun 30th Jul 1st Jul 2nd Jul 5th Jul 6th Jul 7th Jul 8th Jul 9th Jul 12th Jul 13th Jul 14th Jul 15th Jul 16th Jul 19th Jul 20th Jul 21st Jul 22nd Jul 23rd Jul 26th Jul 27th Jul 28th Jul 29th Jul 30th Aug 2nd Aug 3rd Aug 4th Aug 5th Aug 6th Aug 9th Aug 10th Aug 11th Aug 12th Aug 13th Aug 16th Aug 17th Aug 18th Aug 19th Aug 20th Aug 23rd Aug 24th Aug 25th Aug 26th Aug 27th Aug 28th Aug 30th Aug 31st Sep 1st Sep 2nd Sep 3rd Sep 6th Sep 7th Sep 8th Sep 9th Sep 10th Sep 13th Sep 14th Sep 15th Sep 16th Sep 17th Sep 20th Sep 21st Sep 22nd Sep 23rd Sep 24th Sep 27th Sep 28th Sep 29th Sep 30th Oct 1st Oct 4th Oct 5th Oct 6th Oct 7th Oct 8th Oct 11th Oct 12th Oct 13th Oct 14th Oct 15th Oct 18th Oct 19th Oct 20th Oct 21st Oct 22nd Oct 23rd Oct 25th Oct 26th Oct 27th Oct 28th Oct 29th Nov 1st Nov 2nd Nov 3rd Nov 4th Nov 5th Nov 8th Nov 9th Nov 10th Nov 11th Nov 12th Nov 15th Nov 16th Nov 17th Nov 18th Nov 19th Nov 22nd Nov 23rd Nov 24th Nov 25th Nov 26th Nov 29th Nov 30th Dec 1st Dec 2nd Dec 3rd Dec 6th Dec 7th Dec 8th Dec 9th Dec 10th Dec 13th Dec 14th Dec 15th Dec 16th Dec 17th Dec 20th Dec 21st Dec 22nd Dec 23rd Dec 24th Dec 27th Dec 28th Dec 29th Dec 30th Dec 31st
2022
Jan 3rd Jan 4th Jan 5th Jan 6th Jan 7th Jan 10th Jan 11th Jan 12th Jan 13th Jan 14th Jan 17th Jan 18th Jan 19th Jan 20th Jan 21st Jan 24th Jan 25th Jan 26th Jan 27th Jan 28th Jan 31st Feb 1st Feb 2nd Feb 3rd Feb 4th Feb 7th Feb 8th Feb 9th Feb 10th Feb 11th Feb 14th Feb 15th Feb 16th Feb 17th Feb 18th Feb 21st Feb 22nd Feb 23rd Feb 24th Feb 25th Feb 28th Mar 1st Mar 2nd Mar 3rd Mar 4th Mar 7th Mar 8th Mar 9th Mar 10th Mar 11th Mar 12th Mar 14th Mar 15th Mar 16th Mar 17th Mar 18th Mar 21st Mar 22nd Mar 23rd Mar 24th Mar 25th Mar 28th Mar 29th Mar 30th Mar 31st Apr 1st Apr 4th Apr 5th Apr 6th Apr 7th Apr 8th Apr 11th Apr 12th Apr 13th Apr 14th Apr 15th Apr 18th Apr 19th Apr 20th Apr 21st Apr 22nd Apr 25th Apr 26th Apr 27th Apr 28th Apr 29th May 2nd May 3rd May 4th May 5th May 6th May 9th May 10th May 11th May 12th May 13th May 16th May 17th May 18th May 19th May 20th May 23rd May 24th May 25th May 26th May 27th May 30th May 31st Jun 1st Jun 2nd Jun 3rd Jun 6th Jun 7th Jun 8th Jun 9th Jun 10th Jun 13th Jun 14th Jun 15th Jun 16th Jun 17th Jun 20th Jun 21st Jun 22nd Jun 23rd Jun 24th Jun 27th Jun 28th Jun 29th Jun 30th Jul 1st Jul 4th Jul 5th Jul 6th Jul 7th Jul 8th Jul 11th Jul 12th Jul 13th Jul 14th Jul 15th Jul 18th Jul 19th Jul 20th Jul 21st Jul 22nd Jul 25th Jul 26th Jul 27th Jul 28th Jul 29th Aug 1st Aug 2nd Aug 3rd Aug 4th Aug 5th Aug 8th Aug 9th Aug 10th Aug 11th Aug 12th Aug 15th Aug 16th Aug 17th Aug 18th Aug 19th Aug 22nd Aug 23rd Aug 24th Aug 25th Aug 26th Aug 29th Aug 30th Aug 31st Sep 1st Sep 2nd Sep 5th Sep 6th Sep 7th Sep 8th Sep 9th Sep 12th Sep 13th Sep 14th Sep 15th Sep 16th Sep 19th Sep 20th Sep 21st Sep 22nd Sep 23rd Sep 26th Sep 27th Sep 28th Sep 29th Sep 30th Oct 3rd Oct 4th Oct 5th Oct 6th Oct 7th Oct 10th Oct 11th Oct 12th Oct 13th Oct 14th Oct 17th Oct 18th Oct 19th Oct 20th Oct 21st Oct 24th Oct 25th Oct 26th Oct 27th Oct 28th Oct 31st Nov 1st Nov 2nd Nov 3rd Nov 4th Nov 7th Nov 8th Nov 9th Nov 10th Nov 11th Nov 14th Nov 15th Nov 16th Nov 17th Nov 18th Nov 21st Nov 22nd Nov 23rd Nov 24th Nov 25th Nov 28th Nov 29th Nov 30th Dec 1st Dec 2nd Dec 5th Dec 6th Dec 7th Dec 8th Dec 9th Dec 12th Dec 13th Dec 14th Dec 15th Dec 16th Dec 19th Dec 20th Dec 21st Dec 22nd Dec 23rd Dec 26th Dec 27th Dec 28th Dec 29th Dec 30th
2023
Jan 2nd Jan 3rd Jan 4th Jan 5th Jan 6th Jan 9th Jan 10th Jan 11th Jan 12th Jan 13th Jan 16th Jan 17th Jan 18th Jan 19th Jan 20th Jan 23rd Jan 24th Jan 25th Jan 26th Jan 27th Jan 30th Jan 31st Feb 1st Feb 2nd Feb 3rd Feb 6th Feb 7th Feb 8th Feb 9th Feb 10th Feb 13th Feb 14th Feb 15th Feb 16th Feb 17th Feb 20th Feb 21st Feb 22nd Feb 23rd Feb 24th Feb 27th Feb 28th Mar 1st Mar 2nd Mar 3rd Mar 6th Mar 7th Mar 8th Mar 9th Mar 10th Mar 13th Mar 14th Mar 15th Mar 16th Mar 17th Mar 20th Mar 21st Mar 22nd Mar 23rd Mar 24th Mar 27th Mar 28th Mar 29th Mar 30th Mar 31st Apr 3rd Apr 4th Apr 5th Apr 6th Apr 7th Apr 10th Apr 11th Apr 12th Apr 13th Apr 14th Apr 17th Apr 18th Apr 19th Apr 20th Apr 21st Apr 24th Apr 25th Apr 26th Apr 27th Apr 28th May 1st May 2nd May 3rd May 4th May 5th May 8th May 9th May 10th May 11th May 12th May 15th May 16th May 17th May 18th May 19th May 22nd May 23rd May 24th May 25th May 26th May 29th May 30th May 31st Jun 1st Jun 2nd Jun 5th Jun 6th Jun 7th Jun 8th Jun 9th Jun 12th Jun 13th Jun 14th Jun 15th Jun 16th Jun 19th Jun 20th Jun 21st Jun 22nd Jun 23rd Jun 26th Jun 27th Jun 28th Jun 29th Jun 30th Jul 3rd Jul 4th Jul 5th Jul 6th Jul 7th Jul 10th Jul 11th Jul 12th Jul 13th Jul 14th Jul 17th Jul 18th Jul 19th Jul 20th Jul 21st Jul 24th Jul 25th Jul 26th Jul 27th Jul 28th Jul 31st Aug 1st Aug 2nd Aug 3rd Aug 4th Aug 7th Aug 8th Aug 9th Aug 10th Aug 11th Aug 14th Aug 15th Aug 16th Aug 17th Aug 18th Aug 21st Aug 22nd Aug 23rd Aug 24th Aug 25th Aug 28th Aug 29th Aug 30th Aug 31st Sep 1st Sep 4th Sep 5th Sep 6th Sep 7th Sep 12th Sep 13th Sep 14th Sep 15th Sep 18th Sep 19th Sep 20th Sep 21st Sep 22nd Sep 25th Sep 26th Sep 27th Sep 28th Sep 29th Oct 2nd Oct 3rd Oct 4th Oct 5th Oct 6th Oct 9th Oct 10th Oct 11th Oct 12th Oct 13th Oct 16th Oct 17th Oct 18th Oct 19th Oct 20th Oct 23rd Oct 24th Oct 25th Oct 26th Oct 27th Oct 30th Oct 31st Nov 1st Nov 2nd Nov 3rd Nov 6th Nov 7th Nov 8th Nov 9th Nov 10th Nov 13th Nov 14th Nov 15th Nov 16th Nov 17th Nov 20th Nov 21st Nov 22nd Nov 23rd Nov 24th Nov 27th Nov 28th Nov 29th Nov 30th Dec 1st Dec 4th Dec 5th Dec 6th Dec 7th Dec 8th Dec 11th Dec 12th Dec 13th Dec 14th Dec 15th Dec 18th Dec 19th Dec 20th Dec 21st Dec 22nd Dec 25th Dec 26th Dec 27th Dec 28th Dec 29th
2024
Jan 1st Jan 2nd Jan 3rd Jan 4th Jan 5th Jan 8th Jan 9th Jan 10th Jan 11th Jan 12th Jan 15th Jan 16th Jan 17th Jan 18th Jan 19th Jan 22nd Jan 23rd Jan 24th Jan 25th Jan 26th Jan 29th Jan 30th Jan 31st Feb 1st Feb 2nd Feb 5th Feb 6th Feb 7th Feb 8th Feb 9th Feb 12th Feb 13th Feb 14th Feb 15th Feb 16th Feb 19th Feb 20th Feb 21st Feb 22nd Feb 23rd Feb 26th Feb 27th Feb 28th Feb 29th Mar 1st Mar 4th Mar 5th Mar 6th Mar 7th Mar 8th Mar 11th Mar 12th Mar 13th Mar 14th Mar 15th Mar 18th Mar 19th Mar 20th Mar 21st Mar 22nd Mar 25th Mar 26th Mar 27th Mar 28th Mar 29th Apr 1st Apr 2nd Apr 3rd Apr 4th Apr 5th Apr 8th Apr 9th Apr 10th Apr 11th Apr 12th Apr 15th Apr 16th Apr 17th Apr 18th Apr 19th Apr 22nd Apr 23rd Apr 24th
Spot Prices Updated Daily
Updated daily. Spot prices on 23 base metals, precious metals, rare metals and materials PLUS charts and historical prices going back as far as January 2000.
ARCHIVE Browse our metal price archive with metal prices going back to 2000 in USD and back to 2010 in other national currencies and cryptocurrencies.
Metal Facts
Popular Metal Prices
Metal Price Charts
Widgets & Charts for Websites
Get free metal price charts & widgets for your website.
Display metal price tables and and daily spot price charts on your website.
Our responsive widgets and charts scale to nearly any display size.